Quantum Mechanical Model of Atom – Schrödinger Equation

The number of spherical nodes in 3p orbitals are

For radial probability curves, which of the following is/are correct?

Plot of radial wave function $\mathrm{\Psi }\left(\mathrm{r}\right)$ as a function of distance $\mathrm{r}$ of the electron from the nucleus for $1\mathrm{s}$ orbital.

The number of radial nodes in $1\mathrm{s}$ and $2\mathrm{s}$ orbitals are respectively:

The number of nodal planes in $5\mathrm{d}$ orbital is _____.

The number of nodal planes in $5\mathrm{d}$ orbital is

The region of space around the nucleus where the probability of finding an electron is maximum is called_____.

What is the quantum mechanical model of an atom?

_____ developed a quantum mechanical model of an atom.(Rutherford/Erwin Schrodinger)

Do the electrons follow the definite paths around the nucleus?

The number of nodal planes ‘ $5\mathrm{d}$’ orbital has, is:

(Assume that all graphs have been plotted for the same parameters. In all these curves n $< 4$ )

Choose the correct radial probability curve for $3\mathrm{p}-$orbital.

Number of radial nodes for $4\mathrm{f}$ orbital

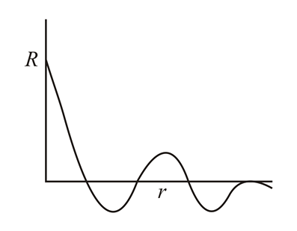
From the following graph between R (radial wave function) and r (distance from nucleus), identify orbital:-

$0.53 A^{\circ }$ is Bohr's radius of the first orbit. In the light of the wave mechanical model, it suggests that 

Choose the correct options:

The radial distribution function $\left[\mathrm{P}\left(\mathrm{r}\right)\right]$ is used to determine the most probable radius which is used to find the electron in a given orbital. The $\frac{\mathrm{d} \left[P\left(\mathrm{r}\right)\right]}{\mathrm{dr}}$ is given by $\frac{\mathrm{d}\left[\mathrm{P} \left(\mathrm{r}\right)\right]}{\mathrm{dr}}= \frac{4{\mathrm{z}}^3}{{\mathrm{a}}_0^3} \left[2\mathrm{r}-\frac{2{\mathrm{Zr}}^2}{{\mathrm{a}}_0}\right] {\mathrm{e}}^{\frac{-2\mathrm{Zr}}{{\mathrm{a}}_0}}$. Then, which of the following statements are correct?

Mr. Santa has to decode a number "ABCDEF" where each alphabet is represented by a single digit. Suppose an orbital whose radial wave function is represented as $\Psi_{(r)}=k_{1} e^{-r / k_{2}}\left(r^{2}-5 k_{3} r+6 k_{3}^{2}\right)$
From the following information given about each alphabet then write down the value of $\{(A \times D)+(B+C+E+F)\}$ where each alphabet corresponds to a value.
Info $\mathrm{A}=$ Value of $\mathrm{n}$ where "n" is principal quantum number
Info $\mathrm{B}=\mathrm{No}$. of angular nodes
Info $\mathrm{C}=$ Azimuthal quantum number of subshell to which orbital belongs Info $\mathrm{D}=$ No. of subshells having energy between $(\mathrm{n}+5) \mathrm{s}$ to $(\mathrm{n}+5) \mathrm{p}$ where $\mathrm{n}$ is principal quantum number
Info $E=$ Orbital angular momentum of given orbital.
Info $\mathrm{F}=$ Radial distance of the spherical node which is farthest from the nucleus (Assuming: $\mathrm{k}_{3}=1$ )

The${\mathrm{Li}}^{2+}$ ion is a hydrogen like ion that can be described by the Bohr model. Calculate the Bohr radius of the third orbit and calculate the energy of an electron in $4$th orbit.